Trực tiếp bóng đá xoilac - Thiên đường xem bóng đá hàng đầu Việt Nam
Trực tiếp bóng đá Xoilac là địa chỉ được nhiều người dùng quan tâm khi muốn theo dõi bóng đá trực tuyến. Theo dõi ngay bài viết để có thêm thông tin chi tiết nhé!
Ngày 23/04/2024
Trực tiếp bóng đá xoilac là website chuyên cung cấp các thông tin về thể thao, những trận đấu trực tiếp hấp dẫn cùng nhiều tiện ích khác. Chính vì thế mà địa chỉ này nhận được nhiều sự quan tâm từ phía cộng đồng người dùng tại Việt Nam. Để có thêm thông tin chi tiết về trang web này, anh em hãy theo dõi tiếp nội dung sau đây nhé!
Trực tiếp bóng đá xoilac - Tổng quan về kênh
Hiện tại cái tên xoilac đã trở nên quá đỗi quen thuộc đối với nhiều người hâm mộ bóng đá tại Việt Nam, tuy nhiên lại ít ai biết được hoàn cảnh ra đời của trang web này.

Lịch sử thành lập kênh xoilac
Bóng đá từ lâu đã trở thành một bộ môn thể thao nhận được sự ưu ái từ hàng triệu người hâm mộ trên khắp thế giới. Do đó mà càng ngày nhu cầu xem bóng đá của mọi người dần nhiều hơn. Trước đây có nhiều gia đình chưa có điều kiện mua tv thì sẽ thường ra ngồi các hàng quán cafe để được tận hưởng không khí xem bóng đá.
Ngày nay với sự phát triển mạnh mẽ của công nghệ thì mọi người có thể dễ dàng theo dõi được các trận đấu mình yêu thích qua máy tính hoặc điện thoại di động. Đây có thể được xem là cách tiện lợi nhất khi không có thời gian để ra ngoài. Hiểu được điều này, đội ngũ phát triển kênh đã nghiên cứu và xây dựng nên một kênh xem bóng đá trực tuyến nhằm giúp người hâm mộ có thể thưởng thức được tất cả các trận đấu đỉnh cao với chất lượng tốt nhất. Từ đó mà cái tên trực tiếp bóng đá xoilac ra đời.
Kể từ khi được thành lập, kênh luôn cố gắng thực hiện tốt nhất phương châm “Không chỉ xem bóng đá trực tuyến mà còn hướng đến sự trải nghiệm bóng đá đỉnh cao một cách đơn giản nhất”. Nhà phát hành đã không ngừng đầu tư, đổi mới đường truyền cũng như nâng cấp độ phân giải video. Nhờ đó mà người hâm mộ có thể cảm nhận được sự chân thực, sống động trong mỗi pha bóng.
Mục tiêu phát triển trong tương lai
Mục tiêu phục vụ số đông người hâm mộ yêu bóng đá là tiêu chí hàng đầu mà kênh trực tiếp bóng đá xoilac đã đặt ra. Tại đây người xem sẽ được tiếp cận mọi trận đấu bóng đá đỉnh cao của đội tuyển Việt Nam cũng như các trận đấu bóng đá quốc tế khác. Anh em có thể tìm kiếm và theo dõi hoàn toàn miễn phí.
Với sự nhiệt huyết, đội ngũ phát triển kênh luôn cố gắng lắng nghe ý kiến từ phía người dùng, qua đó có thể nắm bắt và điều chỉnh kịp thời nhằm tạo ra sự tiện lợi nhất. Tại đây có hàng loạt các giải đấu bóng đá hấp dẫn hàng đầu thế giới như: Anh, Ý, Đức, Tây Ban nha,... Bên cạnh đó kênh còn luôn có một đội ngũ bình luận viên tiếng Việt nhằm tạo nên một không khí bóng đá sôi động và tràn ngập tiếng cười dành cho người hâm mộ sau những ngày làm việc vất vả.
Qua một khoảng thời gian hoạt động, kênh đã dần chiếm trọn được tình cảm của nhiều người hâm mộ bóng đá tại Việt Nam. Xoilac luôn mong muốn người dùng có thể được theo dõi các trận đấu bóng đá một cách trọn vẹn với chi phí phù hợp nhất. Bên cạnh khoản phí internet cần phải đóng hàng tháng thì anh em sẽ không cần phải đóng bất cứ một khoản phí nào khác để xem được bóng đá tại đây. Ngoài ra, những người thành lập kênh cũng đã không ngừng cải tiến, nâng cấp chất lượng video của mình sao cho sống động và chân thực giống như đang ở trực tiếp trên sân.
Những tính năng tại xoilac

Đến với trực tiếp bóng đá xoilac, người dùng không chỉ được thưởng thức các trận đấu bóng đá hấp dẫn mà còn được trải nghiệm các tính năng thú vị như:
Lịch thi đấu
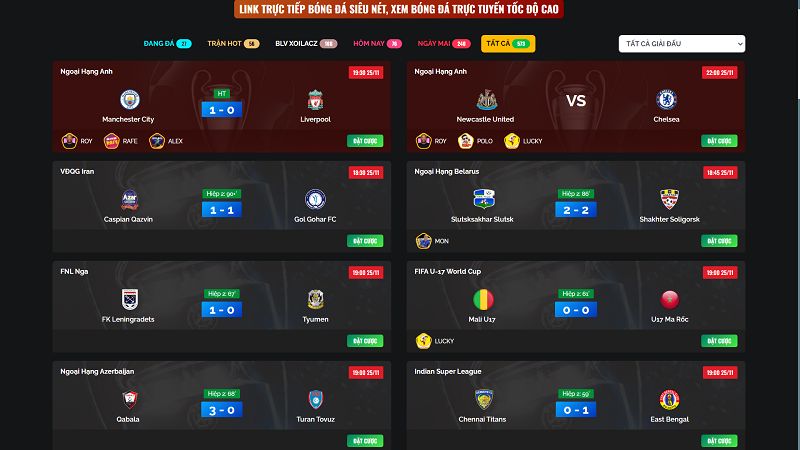
Ngay sau khi truy cập vào đường link trực tiếp bóng đá xoilac, điều đầu tiên mà anh em sẽ nhận thấy đó chính là tính năng lịch thi đấu. Tại đây hội tụ hàng loạt các giải đấu hấp dẫn sẽ được phát sóng trong 7 ngày gần nhất, có đầy đủ thời gian, địa điểm diễn ra trong ngày và đi cùng với đó là khá nhiều thông tin quan trọng khác. Do đó, để tiện theo dõi thì anh em có thể sử dụng tính năng này của kênh và tìm kiếm. Đảm bảo các thông tin cần thiết sẽ được tìm thấy nhanh chóng nhất.
Bảng xếp hạng các giải đấu trên thế giới
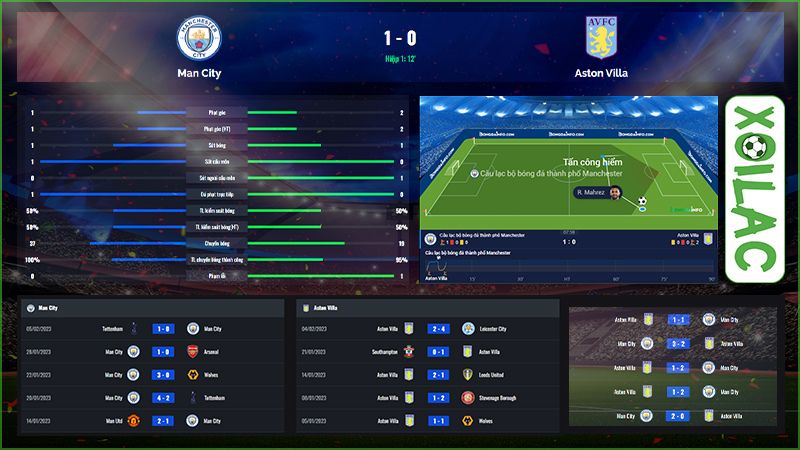
Tại phần tính năng bảng xếp hạng của kênh sẽ cập nhật đầy đủ vị trí của hàng loạt đội bóng thường xuyên xếp top đầu trên bảng xếp hạng và được phân chia theo khu vực, hạng thi đấu cũng như quốc gia khác nhau. Qua đó giúp cho người chơi có thể dễ dàng nắm bắt được tình hình thi đấu của đội bóng mình yêu thích trong các trận gần đây. Với tính năng này, anh em sẽ rất dễ dàng tham gia soi kèo bóng đá và đưa ra được các nhận định chuẩn xác nhất.
Tỷ lệ kèo hoàn toàn miễn phí
Bên cạnh các tính năng kể trên thì tại kênh trực tiếp bóng đá xoilac còn cập nhật nhiều tỷ lệ kèo “hấp dẫn” dành riêng cho anh em cược thủ. Đây đều được chọn lọc từ các nhà cung cấp kèo cược thể thao uy tín và hàng đầu Việt Nam và có chức năng cập nhật tỷ lệ kèo thường xuyên. Mục đích nhằm giúp các thành viên của kênh có thể dễ dàng chốt được kèo đẹp và nắm rõ được tình hình các trận đấu đang diễn ra. Qua đó có thể đưa ra được lựa chọn cá cược thông minh hay dự đoán tỷ số kết quả của trận đấu một cách chính xác và hiệu quả nhất.
Kết quả bóng đá trực tuyến

Trực tiếp bóng đá xoilac còn mang đến cho người dùng tính năng kết quả bóng đá. Tại đây các trận đấu diễn ra trong ngày đều sẽ được cập nhật kết quả chuẩn xác và đầy đủ nhất. Những thông tin như tỷ số bàn thắng, các cầu thủ ghi bàn, thời gian kiểm soát bóng, tổng số bàn thắng ghi được, số lần phạt góc hay số thẻ phạt phải nhận,.. Tất cả đều sẽ được cập nhật đầy đủ và nhanh chóng tại trang chủ. Các thông tin tại đây đều được kênh thẩm định và kiểm tra tính đúng sai kỹ càng trước khi cung cấp cho người xem. Đảm bảo các tin tức nhận được sẽ không bị sai lệch và mang tính khách quan nhất.
Tin tức thể thao được cập nhật liên tục
Trang chủ trực tiếp bóng đá xoilac hiện đã có tính năng cập nhật đầy đủ các tin tức mới nhất về thể thao. Tại đây sẽ cung cấp cho anh em hàng loạt thông tin chi tiết liên quan đến đội tuyển, cầu thủ, huấn luyện viên hay các giải đấu bóng đá hấp dẫn đang diễn ra. Chuyên mục này sẽ được cập nhật mỗi ngày với tin tức từ trong cho đến ngoài nước. Đảm bảo rằng anh em có thể dễ dàng nắm bắt được các tin tức về việc nhượng, vòng loại giải đấu hay các thông tin thú vị khác về bóng đá tại đây một cách dễ dàng và nhanh chóng nhất.
Hướng dẫn các bước xem trực tiếp bóng đá xoilac

Anh em có thể xem trực tiếp bóng đá xoilac một cách đơn giản mà không cần tạo tài khoản. Nhưng để có trải nghiệm tuyệt vời nhất khi xem trực tiếp bóng đá tại đây thì anh em có thể đăng ký trở thành một thành viên chính thức của kênh thông qua các bước đơn giản sau đây:
- Bước 1: Anh em cần phải có thiết bị điện thoại thông minh hoặc máy tính có kết nối internet ổn định.
- Bước 2: Tiếp theo anh em hãy truy cập vào trình duyệt web và bấm “xoilac” để tìm kiếm thông tin của kênh.
- Bước 3: Khi trang web hiện ra thì lúc này anh em có thể thoải mái truy cập được vào các thông tin hay những trận đấu mà mình muốn xem.
Một số lưu ý khi xem trực tiếp bóng đá xoilac

Để có được những trải nghiệm tuyệt vời nhất tại trực tiếp bóng đá xoilac, anh em cần chú ý đến một số vấn đề sau đây:
- Đầu tiên cần phải chuẩn bị một đường truyền hoặc các thiết bị có kết nối internet ổn định. Nhờ vậy mà anh em có thể dễ dàng theo dõi được các trận đấu mình yêu thích một cách dễ dàng ở bất cứ đâu.
- Nếu gặp trường hợp máy bị đơ, cấu hình mạng yếu hay bị load chậm do số lượng người dùng truy cập quá đông. Thì lúc này anh em hãy tiến hành dừng video này lại và bấm tiếp tục để xem tiếp.
- Hiện kênh đang cung cấp thêm một số đường link dự phòng, anh em có thể dễ dàng truy cập vào để tránh tình trạng bị lag giật.
- Người dùng còn có thể tự ý điều chỉnh lượng âm thanh, chất lượng video sao cho phù hợp với yêu cầu của mình một cách dễ dàng.
Một số nhược điểm còn tồn tại ở trực tiếp bóng đá xoilac
Bên cạnh những dịch vụ thể thao cùng chất lượng phát sóng bóng đá hàng đầu tại Việt Nam thì kênh trực tiếp bóng đá xoilac vẫn còn tồn tại một số nhược điểm sau:
- Đầu tiên đây là kênh phát sóng trực tiếp bóng đá không thông qua trung gian nên người dùng có thể sẽ gặp phải tình trạng bị điều hướng trang. Để khắc phục tình trạng này, kênh đã cung cấp thêm nhiều đường link dự phòng khác nhau để anh em có thể dễ dàng truy cập nếu không muốn gặp những trường hợp tương tự.
- Bên cạnh đó, các đường link phát sóng trực tiếp tại đây đôi lúc sẽ gặp lỗi về các vấn đề bản quyền. Do đó kênh sẽ thường xuyên thay các tên miền khác nhau để người dùng có thể truy cập dễ dàng hơn.
Kết luận
Trên đây là những đánh giá chi tiết về kênh trực tiếp bóng đá xoilac. Đây thực sự là một trang web xem bóng đá trực tuyến đáng để anh em tham gia và trải nghiệm. Hãy nhanh tay truy cập link để theo dõi ngay các trận đấu mà mình yêu thích nhé!